Many interesting ecological problems are multivariate and involve complex
relationships among variables. To address these issues, probability networks,
or Bayes nets (Reckhow 1999), are among the most interesting and potentially
useful current research directions for the application of Bayesian methods in
ecology and the environmental sciences.
It is common modeling practice to develop a flow diagram consisting of
“boxes and arrows” to describe relationships among key variables in an aquatic
ecosystem and use this diagram as a device to guide model development and
explanation. In ecology, this “graphical model” is typically used to display
the flow of materials or energy in an ecosystem. For a probability network,
however, the “flows” indicated by the arrows in a graphical model do not
represent material flow or energy flow; rather, they represent conditional
dependency. Thus, while the probability modeling approach of interest here
typically begins with a graphical model, in this case the presence (absence) of
an arrow connecting two boxes specifies conditional dependence (independence).
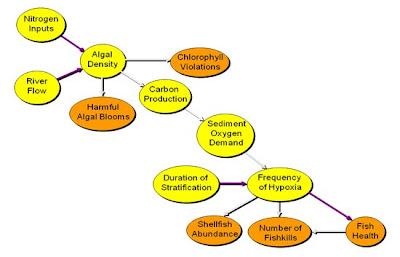
An example is given in the figure below for eutrophication in the Neuse Estuary
in North Carolina (Borsuk et al. 2004).
Probability
networks like that in the figure can be as simple or as complex as scientific
needs, knowledge, and data allow. The relationships may reflect direct causal
dependencies based on process understanding or a statistical, aggregate summary
of more complex associations. In either case, the relationships are
characterized by conditional probability distributions that reflect the
aggregate response of each variable to changes in its “up-arrow” (or parent) predecessor,
together with the uncertainty in that response. In that regards, it is
important to recognize that the conditional independence characterized by
absence of an arrow in a Bayes net graphical model is not the same as complete
independence, a feature that is likely to be quite rare in systems of interest.
For example, ecological knowledge suggests that many of the variables in the figure
are likely to be interrelated or interdependent. However, the arrows in the figure
indicate that conditional on sediment oxygen demand and duration of
stratification, frequency of hypoxia is independent of all other variables.
This means that once sediment oxygen demand and duration of stratification are
known, knowledge of other variables does not change the probability (frequency)
of hypoxia.
Conditional probability relationships
may be based on either (1) observational/experimental data or (2) expert
scientific judgment. Observational data that consist of precise measurements of
the variable or relationship of interest are likely to be the most useful, and
least controversial, information. Unfortunately, appropriate and sufficient
observational data may not always exist. Experimental evidence may fill this
gap, but concerns may arise regarding the applicability of this information to
the natural, uncontrolled system, and appropriate experimental data may also be
limited. As a consequence, the elicited judgment of scientific experts may be
required to quantify some of the probabilistic relationships (see: http://kreckhow.blogspot.com/2013/07/quantifying-expert-judgment-for.html). Of course, the use of subjective judgment is not unusual in water
quality modeling. Even the most process-based computer simulations rely on
subjective judgment as the basis for the mathematical formulations and the
choice of parameter values. Therefore, the explicit use of scientific judgment
in probability networks should be an acceptable practice. In fact, by
formalizing the use of judgment through well-established techniques for expert
assessment, the probability network method may improve the chances of accurate
and honest predictions.
The Bayes
net presented in the figure above as a graphical model was used for development
of the TMDL (total maximum daily load) for nitrogen in the Neuse Estuary to
address water quality standard violations (Borsuk et al. 2003). Several
features of the Bayes net improved the modeling and analysis for the Neuse
nitrogen TMDL. To facilitate explanations and to enhance credibility, the underlying
structure of the Neuse probability network (reflected in the variables and
relationships conveyed in the graphical model) is designed to be consistent
with mechanistic understanding. The relationships in this model are
probabilistic; they were estimated using a combination of optimization
techniques and expert judgment. The predicted responses are also probabilistic,
reflecting uncertainty in the model forecast. This is important, as it allows
computation of a “margin of safety” which is required by the US EPA for the
assessment of a total maximum daily load. In addition, the Bayes net model can
be updated (using Bayes Theorem) as new information is obtained; this supports
adaptive implementation, which is becoming an important strategy for successful
environmental management.
Applications of Bayes nets are becoming more common in the environmental
literature. Reckhow, Borsuk, and Stow (see Reckhow 1999, 2010, and Borsuk et
al. 2003, 2004) present additional details documenting the Neuse Estuary Bayes
net models described above, as well as Bayes nets developed and applied to
address other issues. Software, both commercial and free, is available for
development and application of Bayes nets; some examples are Hugin (http://www.hugin.com/), Netica (http://www.norsys.com/netica.html) BayesiaLab
(http://www.bayesia.us/), and GeNIe
(http://genie.sis.pitt.edu/).
Borsuk, Mark
E., Craig A. Stow, and Kenneth H. Reckhow. 2003. An integrated approach to TMDL
development for the Neuse River estuary using a Bayesian probability network
model (Neu-BERN) . Journal Water
Resources Planning and Management. 129:271-282.
Borsuk, M.E., C.A. Stow, and K.H. Reckhow. 2004. A Bayesian
network of eutrophication models for synthesis, prediction, and uncertainty
analysis. Ecological Modelling. 173:219-239.
Reckhow,
K.H. 2010. Bayesian Networks for the Assessment of the Effect of Urbanization
on Stream Macroinvertebrates. Proceedings IEEE Computer Society Press.
HICSS-43. Kauai, Hawaii.
No comments:
Post a Comment